9. Additional Problem Formulations¶

9.1. Discrete-time linear with disturbances¶

E.g., described in [FDLOM16], [WTOXM11], [W10].

9.1.1. Problem description¶

9.1.1.1. System model¶

Consider a system model S with a set V = S U E of variables where S and E are disjoint sets that represent, respectively, the set of plant variables that are regulated by the planner-controller subsystem and the set of environment variables whose values may change arbitrarily throughout an execution.

The domain of V is given by dom(V) = dom(S) x dom(E) and a state of the system can be written as v = (s, e) where

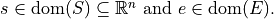
$s \in \text{dom}(S) \subseteq \mathbb{R}^n \text{ and } e \in \text{dom}(E).$

Call s the controlled state and e the environment state.

Assume that the controlled state evolves according to the following discrete-time linear time-invariant state space model: for 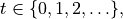$t \in \{0, 1, 2, \ldots\},$

$\begin{array}{rcl} s[t+1] &=& As[t] + Bu[t] + Ed[t]\\ u[t] &\in& U\\ d[t] &\in& D\\ s[0] &\in& \text{dom}(S) \end{array}$

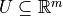where $U \subseteq \mathbb{R}^m$ is the set of admissible control inputs, 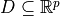$D \subseteq \mathbb{R}^p$ is the set of exogenous disturbances and $s[t],~u[t]$ and $d[t]$ are the controlled state, the control signal, and the exogenous disturbance, respectively, at time t.

9.1.1.2. System specification¶

The system specification 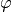$\varphi$ consists of the following components:

the assumption 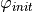$\varphi_{init}$ on the initial condition of the system,
the assumption 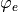$\varphi_e$ on the environment, and
the desired behavior 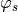$\varphi_s$ of the system.

Specifically, 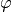$\varphi$ can be written as

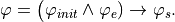
$\varphi = \big(\varphi_{init} \wedge \varphi_e) \rightarrow \varphi_s.$

In general, 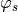$\varphi_s$ is a conjunction of safety, guarantee, obligation, progress, response and stability properties; 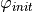$\varphi_{init}$ is a propositional formula; and 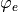$\varphi_e$ is a conjunction of safety and justice formula.

9.1.1.3. Planner-Controller Synthesis Problem¶

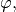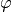Given the system model S and the system specification $\varphi,$ synthesize a planner-controller subsystem that generates a sequence of control signals $u[0], u[1], \ldots \in U$ to the plant to ensure that starting from any initial condition, $\varphi$ is satisfied for any sequence of exogenous disturbances $d[0], d[1], \ldots \in D$ and any sequence of environment states.

9.1.2. Solution strategy¶

We follow a hierarchical approach to attack the Planner-Controller Synthesis Problem:

Construct a finite transition system D (e.g. a Kripke structure) that serves as an abstract model of S (which typically has infinitely many states);
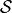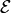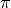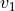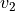- To construct a finite transition system D from the physical model S, we first partition dom(S) and dom(E) into finite sets ${\mathcal S}$ and ${\mathcal E}$ , respectively, of equivalence classes or cells such that the partition is proposition preserving. Roughly speaking, a partition is said to be proposition preserving if for any atomic proposition $\pi$ and any states $v_{1}$ and $v_{2}$ that belong to the same cell in the partition, 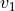$v_{1}$ satisfies 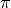$\pi$ if and only if 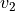$v_{2}$ also satisfies 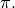$\pi.$ Denote the resulting discrete domain of the system by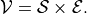 $\mathcal{V} = \mathcal{S} \times \mathcal{E}.$
- The transitions of D are determined based on the following notion of finite time reachability. Let 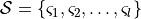$\mathcal{S} = \{ \varsigma_{1},\varsigma_{2}, \ldots, \varsigma_{l} \}$ be a set of discrete controlled states. Define a map 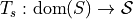$T_{s} : \text{dom}(S) \rightarrow \mathcal{S}$ that sends a continuous controlled state to a discrete controlled state of its equivalence class.
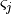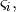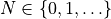- A discrete state $\varsigma_{j}$ is said to be reachable from a discrete state $\varsigma_{i},$ only if starting from any point $s[0] \in T^{-1}_{s}(\varsigma_i),$ there exists a horizon length $N \in \{0, 1, \ldots\}$ and a sequence of control signals $u[0], u[1], \ldots, u[N-1] \in U$ that takes the system to a point $s[N] \in T^{-1}_{s}(\varsigma_j)$ satisfying the constraint $s[t] \in T^{-1}_{s}(\varsigma_i) \cup T^{-1}_{s}(\varsigma_j), \forall t \in \{0, \ldots, N\}$ for any sequence of exogenous disturbances $d[0], d[1], \ldots, d[N-1] \in D.$ In general, for two discrete states, establishing the reachability relation is hard because it requires seaching for a proper horizon length $N.$ 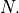In the restricted case where the horizon length is prespecified and 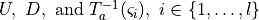$U,~D, \text{ and } T^{-1}_{a} (\varsigma_i),~i \in\{1,\ldots,l\}$ are polyhedral sets, one can establish the reachability relation by solving a affine feasibility problem equivalent to computing the projection of a polytope on to a lower dimensional coordinate aligned subspace.
Synthesize a discrete planner that computes a discrete plan satisfying the specification 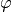$\varphi$ based on the abstract, finite-state model D;
Design a continuous controller that implements the discrete plan.