4. Specifications¶

Currently the best support available in TuLiP is for specifications expressed as GR(1) formulae, which constitutes a sublanguage of LTL. Nonetheless, a more general LTL specification string is described in the below section TuLiP LTL syntax, and it is supported through the class tulip.spec.LTL. Consult Installation (specifically, Alternative discrete synthesis tools) about alternative solvers if you are interested in languages that are not equivalent to GR(1).

4.1. Getting started¶

To create an empty LTL formula and print it, try

from tulip.spec import LTL
f = LTL()
print(f)

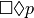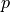The GR(1) formula $\square \Diamond p$ , in which the environment is empty (so, there is no “assumption” part of the specification), and where $p$ is Boolean and controlled, can be created and printed as a specification string (cf. TuLiP LTL syntax) by

from tulip.spec import GRSpec
f = GRSpec(sys_vars={"p"}, sys_prog=["p"])
print(f.dumps())

The result of which should look similar to

0  # Version

%%
OUTPUT:
p : boolean;

%%
[]<>(p)

If you are only interested in the formula itself, presented minimally or with pretty-formatting, then also try

print(f)
print(f.pretty())

The result of the second line (using pretty()) should look similar to

ENVIRONMENT VARIABLES:
        (none)

SYSTEM VARIABLES:
        p     boolean

FORMULA:
ASSUMPTION:
GUARANTEE:
    LIVENESS
          []<>(p)

4.2. TuLiP LTL syntax¶

The LTL syntax defined in EBNF below can be parsed by tulip.spec.lexyacc:

expr ::=
       (* arithmetic operators *)
       | expr '*' expr  (* multiplication *)
       | expr '/' expr  (* division *)
       | expr '+' expr  (* addition *)
       | expr '-' expr  (* subtraction *)
       | expr '<<>>' NUMBER  (* truncation of numbers *)

       (* equality in set theory *)
       | expr '=' expr

       (* negation of `=` *)
       | expr '/=' expr
       | expr '!=' expr
       | expr '^' expr

       (* comparison in arithmetic *)
       | expr '<=' expr
       | expr '=<' expr

       (* comparison in arithmetic *)
       | expr '>=' expr

       (* logical negation *)
       | '~' expr
       | '!' expr

       (* conjunction *)
       | expr '/\' expr
       | expr '&' expr
       | expr '&&' expr

       (* disjunction *)
       | expr '\/' expr
       | expr '|' expr
       | expr '||' expr

       (* logical implication *)
       | expr '=>' expr
       | expr '->' expr

       (* logical equivalence *)
       | expr '<=>' expr
       | expr '<->' expr

       (* ternary conditional
          ("if" expression) *)
       | '(' 'ite' expr ',' expr ',' expr ')'

       (* "next" action operator *)
       | expr "'"
       | 'X' expr
       | 'next' expr

       (* "always" temporal operator *)
       | '[]' expr
       | 'G' expr

       (* "eventually" temporal operator *)
       | '<>' expr
       | 'F' expr

       (* "until" temporal operator *)
       | expr 'U' expr

       (* "release" temporal operator *)
       | expr 'R' expr

       (* parentheses *)
       | '(' expr ')'

       (* Boolean constants *)
       | TRUE
       | FALSE

       (* integral numeralic literals *)
       | NUMBER

       (* identifiers *)
       | variable

       (* string literals *)
       | string

variable ::= NAME

string ::= '"' NAME '"'

where:

NAME can be any alphanumeric other than next that does not start with any character from 'F', 'G', 'R', 'U', 'X'.
NUMBER any non-negative integer
TRUE is case-insensitive 'true'
FALSE is case-insensitive 'false'
(* and *) delimit comments to the above grammar
a number of operators are of TLA+

The token precedence (lowest to highest) and associativity (r = right, l = left, n = none) is:

<=>, <-> (l)
=>, -> (l)
^ (l)
/, | (l)
/**, **& (l)
[], <> (l)
U, W, R (l)
=, /=, != (l)
<=, =<, >=, > (l)
+, - (l)
*, / (l)
~, ! (r)
X (r)
‘ (l)
TRUE, FALSE

Expressions of the above form are successfully parsed. This does not mean that they can be used to produce valid output to be fed to specific solvers. In other words the parser is more permissive than what each tool (and others to be added in the future) supports.

For example: variable '+' variable is valid as parser input, but may be invalid when passed to a particular solver.

4.2.1. Full operator names¶

If you would like to use as operators strings like: and, then your input can be converted automatically to the above syntax by the following lexical substitutions:

next -> X
always -> []
eventually -> <>
until -> U
stronguntil -> U
weakuntil -> W
unless -> W
release -> V
implies -> ->
equivalent -> <->
not -> !
and -> &&
or -> ||

These substitutions are not enabled by default. In order to enable them, pass the argument full_operators = True to tulip.spec.parser.parser.

4.3. TuLiP LTL specification files¶

The description of format here is normative. While details may vary among versions of the format, it is always the case that the first non-blank line must be the version number, which is a non-negative integer.

4.3.1. Version 0¶

An LTL specification file must consist of three sections, which are separated by %%. The first section is referred to as the preamble, the second as the declarations section, and the third as the formula section. Comments can appear anywhere, are begun with #, and continue to the end of the line. Entirely blank lines are ignored. In the preamble, the first non-blank line must be the version number, which is a non-negative integer.

In the declarations section, there are two optional keywords that may appear in any order: INPUT: and OUTPUT:. If given, each must appear on its own line, with no variable declarations. All variable declarations following INPUT:, up to the appearance of OUTPUT: or %%, are taken to be “input variables”, sometimes called uncontrolled or part of the “environment”. All variable declarations following OUTPUT:, up to the appearance of INPUT: or %%, are taken to be “output variables”, sometimes called controlled or part of the “system”. The default behavior (i.e., if these keywords are omitted) is that of OUTPUT:.

A variable declaration is of the form name : domain;. It may span multiple lines. The domain may be

boolean, if the variable (i.e., atomic proposition) can either be True or False;
[a,b], where a and b are integers; or
{...}, where ... is a comma-separated list. The parser will attempt to cast each element as an integer; if it fails, then the element is saved verbatim as a string.

Everything appearing after the second %%, excepting comments, is considered to be part of the LTL formula. Much of the syntax is taken from the LTL formula syntax of Spin. While it will later be expressed by a (Extended?) BNF grammar, the formula syntax is descibed in the following.

An identifier is of the form [a-zA-Z_][a-zA-Z0-9_.]* Note that we do not restrict identifiers from beginning with operator keywords, e.g., X because of the spacing requirement (see below).
True and False are Boolean constants. No variable (identifier) can be thus named.
Boolean operators are ! (negation), && (conjunction), || (disjunction), -> (implication), and <-> (equivalence).
Temporal operators are [] (always), <> (eventually), X (next), U (until), V or R (release).
Notice that the alternative operators /\ and \/ for && and ||, respectively, are not included; cf. the Spin LTL formula syntax. Furthermore, W (weak until) is not included, except for the parser of the GR(1) fragment.
Space is required wherever its absence would cause parsing ambiguity. E.g., Xp is always an identifier, whereas X p is a formula in which the next operator is applied to the identifier p.
Let u and v be variables over integer domains, and let k be an integer. Then “basic comparisons” are u < v, u = v, u < k, and u = k. The following derived operators are also available, with their meaning matching that of the C language: <=, >, >=, !=. Addition within comparisons, given in the form u < v+k or u = v+k, is available, along with derived comparisons as in the previous item. Subtraction is similarly supported; replace + with -.

4. Specifications¶

4.1. Getting started¶

4.2. TuLiP LTL syntax¶

4.2.1. Full operator names¶

4.3. TuLiP LTL specification files¶

4.3.1. Version 0¶

Table of Contents

Previous topic

Next topic

This Page